GEOMETRIA NO EUCLIDIANA, GEOMETRIA PROYECTIVA Y FUNDAMENTOS DE LA GEOMETRIA
GEOMETRIA NO EUCLIDIANA, GEOMETRIA PROYECTIVA Y FUNDAMENTOS DE LA GEOMETRIA
GEOMETRIA NO EUCLIDIANA

La geometría vivió una auténtica revolución con el
surgimiento de geometrías no euclidianas. Todo giraba alrededor del postulado
de las paralelas de Euclides. Después de muchos años de tratar de demostrar el
quinto postulado como una derivación de los otros postulados o de sustituirlo
por otros, se asumió su independencia. Con ello se daría una importante
transformación en la percepción de las matemáticas, en particular sobre su
naturaleza.
Fueron Gauss, el ruso Nikolai Ivanovich Lobachevsky (1793 -
1856) y el húngaro János Bolyai (1802 - 1860), los creadores de las geometrías
no euclidianas, de una manera independiente. Se sabe, gracias a su diario, que
Gauss se había adelantado a los otros matemáticos, pero este matemático no
había publicado sus resultados. Gauss empezó a trabajar en la geometría no
euclidiana desde 1792, con 15 años, cuando le mencionó a un amigo, Schumacher,
la idea de una geometría válida sin el quinto postulado.
En una carta dirigida al matemático húngaro Wolfgang Farkas
Bolyai (1775 - 1856), en 1799, Gauss afirmó que no se podía deducir el quinto
postulado de los otros postulados euclidianos. Desde ese momento con mayor
interés le dedicó sus esfuerzos a geometrías sin ese postulado: por lo menos
desde 1813, Gauss trabajó en la nueva geometría que llamó primero
anti-euclidiana, luego astral y después no euclidiana. Gauss llegó a la
conclusión de que no podía probarse que los resultados de la geometría
euclidiana fueran autoevidentes y su verdad necesaria, lo que sí sucedía -en su
opinión- con la aritmética.
En la geometría que desarrolló Gauss, la suma de los ángulos
de un triángulo es menor que 180 grados, pero esta suma aumenta de acuerdo con
el tamaño del área del triángulo: conforme el área del triángulo se hace más
pequeña, e incluso tiende a 180 cuando el área tiende a 0.
Lobachevsky, hijo de un modesto funcionario del gobierno
ruso, empezó a los 21 años como profesor de la Universidad de Kazán,
institución de la cual llegó a ser rector en 1827. Ya en el año 1826 había
ofrecido su visión y resultados en la nueva geometría, pero este trabajo se
perdió. Tiempo después publicó sus trabajos en Kazan, y también en el Journal
für Mathematik, con un primer ensayo que se llamó "Sobre los fundamentos
de la geometría'' (1829 - 1830) y, luego, un segundo trabajo: "Nuevos
Fundamentos de la Geometría con una Teoría Completa de las Paralelas'' (1835 -
1837). Lobachevsky llamó su geometría en un principio imaginaria y posteriormente
pangeometría.
Bolyai, hijo del profesor húngaro de matemáticas Wolfgang
(Farkas) Bolyai (amigo de Gauss) publicó, en 1832 - 1833, "Ciencia
absoluta del espacio", como apéndice en un libro de Farkas: Tentamen
Juventutem Studiosam in Elementa Matheseos Purae Introducenci (Intento de
introducir la juventud estudiosa en los elementos de Matemáticas Puras). Bolyai
había trabajado las geometrías no euclidianas por lo menos desde 1823, sin
embargo, publicó sus resultados después que Lobachevsky.
Gauss, Lobachevsky y Bolyai asumieron que el postulado
euclidiano de las paralelas no se podía probar como deducción de los otros 9
postulados y axiomas de la geometría euclidiana, y que por eso mismo se
requería un postulado adicional para ofrecer un fundamento a la nueva
geometría. Lo que se hizo fue lo siguiente: puesto que el postulado de las
paralelas era un hecho independiente, se adoptó una proposición contraria a ese
axioma, para entonces deducir las consecuencias en un nuevo sistema con el
nuevo axioma.
Como ha sucedido en otras ocasiones en las que se dan
resultados casi idénticos o similares en un tema, se dio una polémica acerca de
la prioridad histórica de los resultados. Gauss al leer en 1832 el artículo de
János escribió a Farkas diciéndole que no podía aplaudir ese trabajo porque de
hacerlo sería aplaudir su propio trabajo (de Gauss). Bolyai también pensó que
Lobachevsky le había plagiado su trabajo. Fue Lobachevsky el primero en
publicar su obra, y, por eso, se le suele considerar como el padre de la geometría
no euclidiana. El tema estaba en el ambiente matemático de la época, en un
contexto de profundas reformas y cambios sociales y culturales, y existía una
tradición de trabajos precedentes que los tres matemáticos habían podido
considerar: Saccheri, Lambert, Schweikart y Taurinus.
Aunque la geometría no euclidiana constituía una verdadera
revolución, su influencia en la comunidad matemática no fue inmediata. Por un
lado, porque el mismo Gauss no publicó sus resultados y, por el otro, porque
Lobachevsky y Bolyai no eran originarios de los países "importantes'' en
las ciencias y matemáticas de la época. Además, Lobachevsky publicó primero en
ruso y los rusos que lo leyeron fueron muy duros con su trabajo. No fue sino
hasta 1840 que Lobachevsky publicó en alemán. Hay que decir, además, que
durante esa época la geometría de moda era la proyectiva, y, por otra parte,
los matemáticos no se sentían a gusto con ideas tan radicales y novedosas.
Después de la muerte de Gauss, en 1855, se publicó sus
trabajos incluyendo notas y correspondencia en torno a la geometría no
euclidiana. Esto hizo que se le pusiera atención al tema.
Los trabajos de Bolyai y Lobachevsky fueron mencionados en
1866 - 1867 por el matemático Richard Baltzer (1818 - 1887) y poco después se fue
tomando conciencia de la trascendencia de la nueva geometría. La geometría que
desarrollaron asumió que por un punto exterior a una recta pasan un número
infinito de rectas paralelas a la dada (es decir que no poseen puntos de
intersección). Esto se derivaba de la hipótesis del ángulo agudo de Saccheri.
De hecho, es con dos paralelas que trabajó Lobachevsky.
Una valoración de las geometrías no euclidianas y su impacto
en la naturaleza de las matemáticas:
"Al dar el hecho histórico escueto de que Lobachewsky
en 1826 - 9 y J. Bolyai en 1833 casi simultáneamente y con entera independencia
publicaron detallados desarrollos de la geometría hiperbólica, hemos recordado
una de las mejores revoluciones del pensamiento. Para encontrar otra que se le
pueda comparar en importancia de largo alcance hemos de remontarnos a
Copérnico, y aún esta comparación es inadecuada en ciertos aspectos, ya que la
geometría no euclidiana y el álgebra abstracta habrían de cambiar toda la
perspectiva del razonamiento deductivo y no limitarse simplemente a ampliar o a
modificar secciones particulares de la ciencia y de las matemáticas. Al álgebra
abstracta de 1830 y años siguientes, y a las atrevidas creaciones de
Lobachewsky y de Bolyai se remontan el concepto actual (1945) de las matemáticas
como creación arbitraria de los matemáticos. Exactamente de la misma manera que
un novelista inventa personajes, diálogos y situaciones de las que es a la vez
autor y señor, el matemático imagina a voluntad los postulados sobre los que se
basa sus sistemas matemáticos. Tanto el novelista como los matemáticos pueden
estar condicionados por el medio ambiente por la condición y por la manera de
tratar su material; pero ni unos ni otros se ven obligados por ninguna
necesidad eterna y extrahumana a crear ciertos personajes o a inventar ciertos
sistemas. Y si el caso fuera que sí están así condicionados, nadie lo ha
demostrado, y para una inteligencia adulta del siglo XX la multiplicación de
las hipótesis superfluas y místicas es una empresa aún más fútil de lo que lo
era en los días de Occam.'' [Bell, E.T.: Historia de las matemáticas, pp.
342-343]
Realmente las geometrías no euclidianas serían integradas a
las líneas centrales de las matemáticas hasta Riemann, quien contribuyó
directamente a la generación de nuevas geometrías de una forma muy amplia. De
igual manera que Gauss, Bolyai y Lobachevsky Riemann asumió un postulado
contrario al quinto de Euclides, pero lo hizo de una manera diferente. En lugar
de asumir que existe un número infinito de rectas paralelas que pasan por un
punto exterior a una recta dada, asumió que no pasaba ninguna. Puesto de otra
forma: al extenderse indefinidamente las rectas, tarde o temprano éstas se
deberían cortar. Esta era la hipótesis del ángulo obtuso de Saccheri.
Pero Riemann fue más lejos: no solo dudó del quinto
postulado de Euclides sino que de los otros, en particular el segundo. Riemann
consideró que lo que realmente podemos garantizar no es una recta infinita,
sino más bien que el proceso de extender un segmento es sin fin. Hizo una
distinción muy sutil entre longitud infinita y longitud ilimitada o inacabable.
Por ejemplo: uno puede recorrer un círculo ilimitadamente pero el círculo posee
una longitud finita. De esta manera, Riemann enfatizó una dimensión especial
del concepto de recta; éstas aquí no son longitudes infinitas sino ilimitadas.
Usando esta modificación en los postulados creó una nueva
geometría no euclidiana.
Para que se tenga idea de las diferencias, repetimos: en la
geometría de Gauss la suma de los ángulos de un triángulo es menor que 180
grados, mientras que en la de Riemann es mayor que 180. En ambas geometrías la
suma varía según el área del triángulo. Y cuando el área del triángulo tiende a
0: en la de Gauss la suma tiende a 180 grados, en la de Riemann la suma se
acerca por arriba. En ambos casos, para triángulos pequeños, entonces, la suma
ronda los 180, como también sucede en la geometría euclidiana.
Sobre la geometría esférica, hagamos intervenir una bella
explicación dada por Poincaré:
"Imaginemos un mundo poblado únicamente por seres
carentes de espesor; y supongamos que estos animales 'infinitamente chatos'
estén todos en un mismo plano y no puedan salir de él. Admitamos, además, que
ese mundo esté suficientemente alejado de los otros para estar sustraído a su
influencia. Si estamos dispuestos a hacer hipótesis, no nos cuesta nada dotar
de razonamiento a esos seres y considerarlos capaces de construir una
geometría. En ese caso, ciertamente atribuirán al espacio sólo dos dimensiones.
Pero supongamos ahora que esos animales imaginarios, aun
permaneciendo siempre carentes de espesor, tengan la forma de una figura
esférica y no de esfera, sin poder alejarse de ella. ¿Qué geometría podrán
construir? En primer lugar, es evidente que atribuirán al espacio sólo dos
dimensiones; lo que desempeñará para ellos el papel de la recta, será la distancia
más corta de un punto a otro de la superficie esférica, es decir un arco de
círculo máximo; en una palabra, su geometría será la geometría esférica.''
[Poincaré, Henri: Filosofía de la ciencia, p. 175]
Pseudoesfera.
El italiano Beltrami desarrolló una construcción de la
pseudoesfera, superficie donde la curvatura de Gauss es negativa; un método
que, en esencia, demostraba, al igual que la visión proyectiva de Klein, que la
geometría no euclidiana era igualmente consistente que la euclidiana.
GEOMETRIA PROYECTIVA
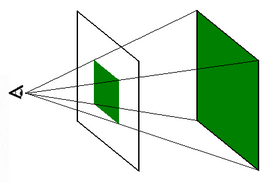
En todo esto, el asunto planteado primeramente por Alberti,
del comportamiento de las proyecciones de una figura, tan cercano a los
trabajos de perspectiva, también fue relevante. Los métodos que se
desarrollaron formaron una disciplina en sí misma.
Fue Girard Desargues (1591 - 1661) el primero en abordar
trabajos en esta dirección. Creó nuevos métodos y conceptos, y a través de la
proyección y la sección como método de prueba abordó diferentes estudios de las
secciones cónicas de una manera general. Su nueva interpretación de la
geometría ofreció una nueva visión sobre esta disciplina. Ya en el año 1636
este arquitecto de la ciudad francesa de Lyon había escrito un libro sobre
perspectiva. Sin embargo, será en 1639 que ofrecerá los conceptos fundamentales
de la geometría proyectiva: Brouillon projet d'une atteinte aux évenements des
rencontres d'un cone avec un plan.
Se afirma, sin embargo, que fue Blaise Pascal (1623 - 1662)
quien más contribuyó a la geometría proyectiva en esta época. El trabajo de
Blaise Pascal también se asoció a las probabilidades, a un famoso teorema de un
hexágono inscrito en un círculo, al triángulo aritmético formado por
coeficientes binomiales, al principio de inducción completa así como a asuntos
propiamente de los infinitesimales.
También se puede citar el trabajo de Philippe de La Hire
(1640 - 1718).
Los trabajos en geometría proyectiva contribuyeron en la
búsqueda de métodos generales en las demostraciones matemáticas, usando
procedimientos más amplios que los de Apolonio, por ejemplo. Esta disciplina
estuvo vinculada a los asuntos de perspectiva de los pintores y al uso de las
secciones cónicas.
Ahora bien, durante el siglo XVII el interés fundamental de
los matemáticos no recayó en la geometría proyectiva, sobre todo porque lo más
relevante eran, por un lado, la potencia de los métodos algebraicos en la
solución de los múltiples problemas científicos y, por el otro, las
aplicaciones. Los trabajos en la geometría proyectiva volverían a retomarse
hasta el siglo XIX. Esto lo comenta Bell, en términos comparativos con la
lógica simbólica:
"La evolución de la geometría proyectiva sintética y de
la lógica simbólica constituye un contraste interesante de supervivencia de lo
anticuado en matemáticas. De ambas nos ocuparemos en capítulos posteriores; por
ahora nos limitaremos a señalar la notable diferencia que existe entre su
suerte y la prosperidad uniforme de otras creaciones del siglo XVII. La
geometría proyectiva sintética, después de que la inventaron Desargues y
Pascal, languideció hasta principios del siglo XIX, en que se hizo muy popular
entre los geómetras que no gustaban del análisis. El sueño de Leibniz de una
ciencia matemática de la deducción quedó adormecido hasta mediados del siglo
XIX, y aún entonces atrajo muy pocos, aunque Leibniz había previsto la
importancia que había de tener la lógica simbólica para toda la matemática, e
hizo personalmente considerables progresos hacia un álgebra de las clases. Tan
solo en la segunda década del siglo XX consiguió la lógica matemática rango de
capítulo principal de las matemáticas.'' [Bell, E.T.: Historia de las
matemáticas, p. 145]
FUNDAMENTOS DE LA GEOMETRIA 
La historia del origen de la Geometría es muy similar a la
de la Aritmética, siendo sus conceptos más antiguos consecuencia de las
actividades prácticas. Los primeros hombres llegaron a formas geométricas a
partir de la observación de la naturaleza.
El sabio griego Eudemo de Rodas, atribuyó a los egipcios el
descubrimiento de la geometría, ya que, según él, necesitaban medir
constantemente sus tierras debido a que las inundaciones del Nilo borraban
continuamente sus fronteras. Recordemos que, precisamente, la palabra geometría
significa medida de tierras.
Los egipcios se centraron principalmente en el cálculo de
áreas y volúmenes, encontrando, por ejemplo, para el área del círculo de radio
unidad un valor aproximado de 3'1605. Sin embargo el desarrollo geométrico
adolece de falta de teoremas y demostraciones formales. También encontramos
rudimentos de trigonometría y nociones básicas de semejanza de triángulos.
También se tienen nociones geométricas en la civilización
mesopotámica, constituyendo los problemas de medida el bloque central en este
campo: área del cuadrado, del círculo, volúmenes de determinados cuerpos,
semejanza de figuras, e incluso hay autores que afirman que esta civilización
conocía el teorema de Pitágoras aplicado a problemas particulares, aunque no,
obviamente, como principio general.
No se puede decir que la geometría fuese el punto fuerte de
las culturas china e india, limitándose principalmente a la resolución de
problemas sobre distancias y semejanzas de cuerpos. También hay quien afirma
que estas dos civilizaciones llegaron a enunciados de algunos casos
particulares del teorema de Pitágoras, e incluso que desarrollaron algunas
ideas sobre la demostración de este teorema.
En los matemáticos de la cultura helénica los problemas
prácticos relacionados con las necesidades de cálculos aritméticos, mediciones
y construcciones geométricas continuaron jugando un gran papel. Sin embargo, lo
novedoso era, que estos problemas poco a poco se desprendieron en una rama
independiente de las matemáticas que obtuvo la denominación de "logística".
A la logística fueron atribuidas: las operaciones con números enteros, la
extracción numérica de raíces, el cálculo con la ayuda de dispositivos
auxiliares, cálculo con fracciones, resolución numérica de problemas que
conducen a ecuaciones de 1er y 2º grado, problemas prácticos de cálculo y
constructivos de la arquitectura, geometría, agrimensura, etc...
Al mismo tiempo ya en la escuela de Pitágoras se advierte un
proceso de recopilación de hechos matemáticos abstractos y la unión de ellos en
sistemas teóricos. Junto a la demostración geométrica del teorema de Pitágoras
fue encontrado el método de hallazgo de la serie ilimitada de las ternas de
números "pitagóricos", esto es, ternas de números que satisfacen la
ecuación a2+b2=c2.

En este tiempo transcurrieron la abstracción y
sistematización de las informaciones geométricas. En los trabajos geométricos
se introdujeron y perfeccionaron los métodos de demostración geométrica. Se
consideraron, en particular: el teorema de Pitágoras, los problemas sobre la cuadratura
del círculo, la trisección de un ángulo, la duplicación del cubo, la cuadratura
de una serie de áreas (en particular las acotadas por líneas curvas).
Paralelamente, al ampliarse el número de magnitudes
medibles, debido a la aparición de los números irracionales, se originó una
reformulación de la geometría, dando lugar al álgebra geométrica. Esta nueva
rama incluía entre otros conceptos el método de anexión de áreas, el conjunto
de proposiciones geométricas que interpretaban las cantidades algebraicas,
división áurea, expresión de la arista de un poliedro regular a través del
diámetro de la circunferencia circunscrita. Sin embargo, el álgebra geométrica
estaba limitada a objetos de dimensión no mayor que dos, siendo inaccesibles
los problemas que conducían a ecuaciones de tercer grado o superiores, es
decir, se hacían imposibles los problemas que no admitieran solución mediante
regla y compás. La historia sobre la resolución de los tres problemas
geométricos clásicos (sobre la cuadratura del círculo, la trisección de un
ángulo, la duplicación del cubo) está llena de anécdotas, pero lo cierto es que
como consecuencia de ellos surgieron, por ejemplo, las secciones cónicas,
cálculo aproximado del número pi, el método de exhaución como predecesor del cálculo
de límites o la introducción de curvas trascendentes.
Asimismo, el surgimiento de la irracionalidad condicionó la
necesidad de creación de una teoría general de las relaciones, teoría cuyo
fundamento inicial lo constituyó el algoritmo de Euclides.
Las primeras teorías matemáticas que se abstrajeron de los
problemas concretos o de un conjunto de problemas de un mismo tipo, crearon las
condiciones necesarias y suficientes para el reconocimiento de la autonomía y
especificidad de las matemáticas.
El carácter abstracto del objeto de las matemáticas y los
métodos de demostración matemática establecidos, fueron las principales causas
para que esta ciencia se comenzara a exponer como una ciencia deductiva, que a
partir de unos axiomas, presenta una sucesión lógica de teoremas. Las obras en
las cuales, en aquella época se exponían los primeros sistemas matemáticos se
denominaban "Elementos".
Se encuentran elementos pertenecientes a muchos autores, sin
embargo todos ellos han quedado relegados a un segundo plano tras la obra
matematica más impresionante de la historia: Los Elementos de Euclides.
"Los Elementos", como denominaremos a esta obra a partir de ahora,
están constituidos por trece libros, cada uno de los cuales consta de una
sucesión de teoremas. A veces se añaden otros dos, los libros 14 y 15 que
pertenecen a otros autores pero por su contenido, están próximos al último
libro de Euclides.
En "Los Elementos" de Euclides se recogen una
serie de axiomas o postulados que sirvieron de base para el posterior
desarrollo de la geometría. Es de especial interés, por la controversia que
originó en épocas posteriores el quinto axioma, denominado "el de las
paralelas", según el cual dos rectas paralelas no se cortan nunca. Durante
siglos se asumió este axioma como irrebatible, hasta que en el siglo XIX
surgieron las llamadas geometrías no euclídeas, que rebatieron este postulado.
Con posterioridad a Euclides y Arquímedes, las matemáticas
cambiaron fuertemente, tanto en su forma como en su contenido, haciendo el
proceso de formación de nuevas teorías más pausado, hasta llegar a
interrumpirse.
Entre las nuevas teorías desarrolladas ocupa el primer lugar
la teoría de las secciones cónicas, que surgió de las limitaciones del álgebra
geométrica. El interés hacia las secciones cónicas creció a medida que
aumentaban la cantidad de problemas resueltos con su ayuda. Sin duda, la obra
más completa, general y sistemática de las secciones cónicas se debe a Apolonio
de Perga.
En la época del dominio romano destacan algunos recetarios
en forma de reglas que permitían el cálculo de algunas áreas y volúmenes; y en
especial la conocida fórmula de Herón para calcular el área del triángulo
conocidos los tres lados.
Durante el primer siglo del Imperio Musulmán no se produjo
ningún desarrollo científico, ya que los árabes, no habían conseguido el
impulso intelectual necesario, mientras que el interés por el saber en el resto
del mundo, había desaparecido casi completamente. Fue a partir de la segunda
mitad del siglo VIII, cuando comenzó el desenfrenado proceso de traducir al
árabe todas las obras griegas conocidas, fundándose escuelas por todo el
Imperio.
Destacaremos como avance anecdótico, pero no por ello
carente de valor, la obtención del número pi con 17 cifras exactas mediante
polígonos inscritos y circunscritos en la circinferencia realizada por Kashi
(s. XV). Después de más de 150 años, en 1593, en Europa, Viète encontró sólo
nueve cifras exactas. Hubo que esperar a fines del siglo XVI y comienzos del
XVII para repetir el cálculo de Kashi.
El rasgo característico más importante de las matemáticas
árabes fue la formación de la trigonometría. En relación con los problemas de
astronomía, confeccionaron tablas de las funciones trigonométricas con gran
frecuencia y alto grado de exactitud, tanto en trigonometría plana como
esférica.
Entre las obras geométricas destacan las de Omar Khayyam (s.
XVI) y Nasir Edin (s. XIII), directamente influenciadas por las obras clásicas,
pero a las que contribuyeron con distintas generalizaciones y estudios
críticos, como los relativos al axioma euclideano del paralelismo, que pueden
considerarse como estudios precursores de la geometría no euclideana.
En el continente europeo, las matemáticas no tienen un
origen tan antiguo como en muchos países del Lejano y Medio Oriente, alcanzando
sólo éxitos notorios en la época del medievo desarrollado y especialmente en el
Renacimiento.
Podemos considerar la obra de Fibonacci "Practica
Geometriae" como el punto de arranque de la geometría renacentista. Esta
obra está dedicada a resolver determinados problemas geométricos, especialmente
medida de áreas de polígonos y volúmenes de cuerpos.
El profesor parisino Nicole Oresmes (1328-1382) llegó a
utilizar en una de sus obras coordenadas rectangulares, aunque de forma
rudimentaria, para la representación gráfica de ciertos fenómenos físicos.
Ya en el siglo XV, época de las grandes navegaciones, la trigonometría
fue separada de la astronomía, alzándose como ciencia independiente de la mano
de Regiomontano (1436-1474), que trató de una manera sistemática todos los
problemas sobre la determinación de triángulos planos y esféricos. Asimismo en
esta obra se establece un notable cambio desde el álgebra literal al álgebra
simbólica.
Fue François Viète (1540-1603) quien dio un sistema único de
símbolos algebraicos consecuentemente organizado, estableciendo en todo
momento, una fuerte conexión entre los trabajos trigonométricos y algebraicos,
de forma que de igual manera que se le considera el creador del álgebra lineal,
se le podría considerar como uno de los padres del enfoque analítico de la
trigonometría, esto es, la goniometría.
Para hacer más fáciles los cálculos, los matemáticos
desarrollaron ciertos procedimientos en los que, el papel fundamental lo
jugaban determinadas relaciones trigonométricas, lo que llevó a la confección
de numerosas tablas trigonométricas. En la elaboración de tablas trabajaron,
por ejemplo, Copérnico (1473-1543) y Kepler (1571,1630). Semejantes métodos se
utilizaban tan frecuentemente que recibieron el nombre de
"prostaferéticos". Ellos fueron utilizados por los matemáticos de
Oriente Medio, Viète, Tycho Brahe, Wittich, Bürgi y muchos otros. Estos métodos
siguieron utilizándose incluso después de la invención de los logaritmos a
comienzos del siglo XVII, aunque sus fundamentos, basados en la comparación
entre progresiones aritméticas y geométricas, comenzaron a fraguarse mucho antes.
Durante el siglo XVII surgieron casi todas las disciplinas
matemáticas, produciéndose en lo que a la geometría se refiere el nacimiento de
la geometría analítica.
Sin duda los dos grandes en esta materia y época fueron René
Descartes (1596-1650) y Pierrede Fermat (1601-1655).

La última parte de la famosa obra de Descartes
"Discurso del Método" denominada "Géometrie", detalla en su
comienzo, instrucciones geométricas para resolver ecuaciones cuadráticas,
centrándose seguidamente en la aplicación del álgebra a ciertos problemas
geométricos. Analiza también curvas de distintos órdenes, para terminar en el
tercer y último libro que compone la obra, con la construcción de la teoría
general de ecuaciones, llegando a la conclusión de que el número de raíces de
una ecuación es igual al grado de la misma, aunque no pudo demostrarlo.
Prácticamente la totalidad de la Géometrie está dedicada a la interrelación
entre el álgebra y la geometría con ayuda del sistema de coordenadas.
Simultáneamente con Descartes, Pierre de Fermat desarrolló
un sistema análogo al de aquél. Las ideas de la geometría analítica, esto es,
la introducción de coordenadas rectangulares y la aplicación a la geometría de
los métodos algebraicos, se concentran en una pequeña obra: "introducción
a la teoría de los lugares planos y espaciales". Aquellos lugares
geométricos representados por rectas o circunferencias se denominaban planos y
los representados por cónicas, especiales. Fermat abordó la tarea de
reconstruir los "Lugares Planos" de Apolonio, describiendo alrededor
de 1636, el principio fundamental de la geometría analítica: "siempre que
en una ecuación final aparezcan dos incógnitas, tenemos un lugar geométrico, al
describir el extremo de uno de ellos una línea, recta o curva". Utilizando
la notación de Viète, representó en primer lugar la ecuación Dx=B, esto es, una
recta. Posteriormente identificó las expresiones xy=k2; a2+x2=ky;
x2+y2+2ax+2by=c2; a2-x2=ky2 con la hipérbola, parábola circunferencia y elipse
respectivamente. Para el caso de ecuaciones cuadráticas más generales, en las
que aparecen varios términos de segundo grado, aplicó rotaciones de los ejes
con objeto de reducirlas a los términos anteriores.
La extensión de la geometría analítica al estudio de los
lugares geométricos espaciales, la realizó por la vía del estudio de la
intersección de las superficies espaciales por planos. Sin embargo, las
coordenadas espaciales también en él están ausentes y la geometría analítica
del espacio quedó sin culminar.
En el siglo XVIII, además de la consolidación de la
geometría analítica, surgieron la geometría diferencial, la geometría
descriptiva y proyectiva, así como numerosos trabajos sobre los fundamentos de
la geometría.
Entre los diferentes problemas y métodos de la geometría,
tuvieron gran significado las aplicaciones geométricas del cálculo
infinitesimal. De ellas surgió y se desarrolló la geometría diferencial, la
ciencia que ocupó durante el siglo XVIII el lugar central en al sistema de las
disciplinas geométricas.
A comienzos de siglo ya habían sido estudiados muchos
fenómenos de las curvas planas por medio del análisis infinitesimal, para pasar
posteriormente a estudiar las curvas espaciales y las superficies. Este
traspaso de los métodos de la geometría bidimensional al caso tridimensional
fue realizado por Clairaut. Sin embargo, su obra fue eclipsada, como casi todo
en esta época, por los trabajos de Euler.
Fue Euler quien, en 1748, sistematizó la geometría analítica
de una manera formal. En primer lugar expuso el sistema de la geometría
analítica en el plano, introduciendo además de las coordenadas rectangulares en
el espacio, las oblicuas y polares. En segundo lugar, estudió las transformaciones
de los sistemas de coordenadas. También clasificó las curvas según el grado de
sus ecuaciones, estudiando sus propiedades generales. En otros apartados de sus
obras trató las secciones cónicas, las formas canónicas de las ecuaciones de
segundo grado, las ramas infinitas y asintóticas de las secciones cónicas y
clasificó las curvas de tercer y cuarto orden, demostrando la inexactitud de la
clasificación newtoniana. También estudió las tangentes, problemas de
curvaturas, diámetros y simetrías, semejanzas y propiedades afines,
intersección de curvas, composición de ecuaciones de curvas complejas, curvas
trascendentes y la resolución general de ecuaciones trigonométricas. Todo estos
aspectos se recogen en el segundo tomo de la obra "Introducción al análisis..."
que Euler dedicó exclusivamente a la geometría analítica.
Los métodos de la geometría descriptiva surgieron en el
dominio de las aplicaciones técnicas de la matemática y su formación como
ciencia matemática especial, se culminó en los trabjos de Monge, cuya obra en
este terreno quedó plasmada en el texto "Géometrie descriptive". En
la obra se aclara, en primer lugar, el método y objeto de la geometría
descriptiva, prosiguiendo a continuación, con instrucciones sobre planos
tangentes y normales a superficies curvas. Analiza en capítulos posteriores la
intersección de superficies curvas y la curvatura de líneas y superficies.
El perfeccionamiento de carácter particular y la elaboración
de diferentes métodos de proyección contituyeron el contenido fundamental de
los trabjos sobre geometría proyectiva en lo sucesivo. La idea del estudio de
las propiedades proyectivas de los objetos geométricos, surgió como un nuevo
enfoque que simplificara la teoría de las secciones cónicas. Las obras de
Desargues y Pascal resuelven este problema y sirven de base a la nueva
geometría.
La geometría hacia comienzos del siglo XIX representaba ya
un amplio complejo de disciplinas surgidas del análisis y generalizaciones de
los datos sobre las formas espaciales de los cuerpos. Junto a las partes
elementales, se incluyeron en la geometría casi todas aquellas partes que la
conforman actualmente.
La geometría analítica realizó un gran camino de desarrollo
y determinó su lugar como parte de la geometría que estudia las figuras y transformaciones
dadas por ecuaciones algebraicas con ayuda del método de coordenadas utilizando
los métodos del álgebra.
La geometría diferencial se caracterizó por la utilización
de los conceptos y métodos del cálculo diferencial, lo que conllevó relaciones
estables con el análisis matemático y con numerosos problemas aplicados.
Una de las características principales de la geometría que
se desarrolló durante la segunda mitad del siglo XIX, fue el entusiasmo con que
los matemáticos estudiaron una gran variedad de transformaciones. De ellas, las
que se hicieron más populares fueron las que constituyen el grupo de
transformaciones que definen la denominada geometría proyectiva. Los métodos
aparentemente detenidos en su desarrollo desde la época de Desargues y Pascal,
de estudio de las propiedades de las figuras invariantes respecto a la
proyección, se conformaron en los años 20 del siglo XIX en una nueva rama de la
geometría: la geometría proyectiva, merced sobre todo a los trabajos de J.
Poncelet.
Otro aspecto esencial durante este siglo fue el desarrollo
de las geometrías no euclideanas. Podríamos considerar fundador de esta
geometría al matemático ruso Nicolai Ivanovich Lobachevski (1792-1856). Su obra
mostraba que era necesario revisar los conceptos fundamentales que se admitían
sobre la naturaleza de la matemática, pero ante el rechazo de sus
contemporáneos tuvo que desarrollar sus ideas en solitario aislamiento.
El punto de partida de las investigaciones de Lobachevski
sobre geometría no euclideana fue el axioma de las paralelas de Euclides, sin
demostración durante siglos. Lobachevski, que inicialmente intentó demostrar
dicho axioma, rápidamente se dio cuenta que ello era imposible, sustituyendo
dicho axioma por su negación: a través de un punto no contenido en una recta se
puede trazar más de una paralela que yace en el mismo plano que la primera.
El año 1826 puede considerarse como la fecha de nacimiento
de esta geometría no euclideana o lobachevskiana, siendo en ese año cuando el
autor presentó muchos de los trabajos que avalaban la nueva teoría.
En 1829 Janos Bolyai (1802-1860) llegó a la misma conclusión
a la que había llegado Lobachevski. E incluso el mismo Gauss que apoyaba y
elogiaba a escondidas, nunca de forma pública, los trabajos de Bolyai y
Lobachevski, es posible que mantuviera los mismos puntos de vista pero los
calló por temor a comprometer su reputación científica.

La geometría no euclideana continuó siendo durante varias
décadas un aspecto marginal de la matemática, hasta que se integró en ella
completamente gracias a las concepciones extraordinariamente generales de
Rieman.